# 双指针

# 1、盛最多水的容器

题目：给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

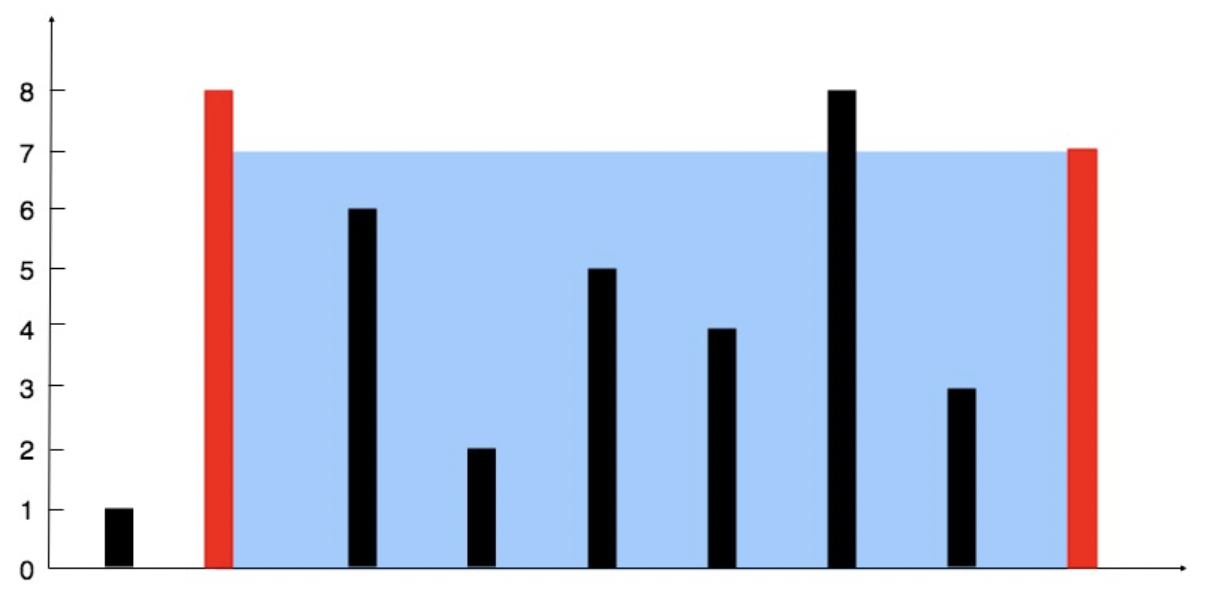
解题思路：area = min(height(x), height(y)) * (y - x);

# 1、暴力枚举

时间复杂度：o(n^2)

空间复杂度：o(1)

var maxArea = function(height) {
    const lenght = height.length;
    if(height == null || lenght < 2){
        return 0
    }
    let maxNum = 0;
    for(let i=0; i<lenght; i++){
        for(let j=i+1; j<lenght; j++){
            const num = Math.min(height[i], height[j])*(j - i);
            if(num > maxNum) maxNum = num;
        }
    }
    return maxNum;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 2、双指针

时间复杂度：o(n)

空间复杂度：o(1)

var maxArea = function(height) {
    const length = height.length;
    if(height == null || length < 2){
        return 0
    }
    let left = 0, right = length -1;
    let maxNum = 0;
    while(left < right){
        const num = Math.min(height[left], height[right])*(right - left);
        if(num > maxNum){
            maxNum = num;
        }
        if(height[left]<height[right]){
            left++;
        }else{
            right--;
        }
    }
    return maxNum;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 2、接雨水

题目：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

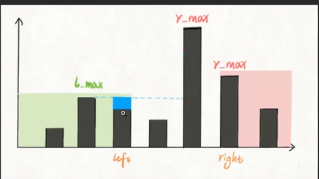
解题思路：当前柱子能接的雨水 = min(左边最高柱子，右边最高柱子) - 当前柱子高度

# 1、暴力枚举

时间复杂度：O(n^2)
空间复杂度：O(1)

function trap(height = []){
    if(height.length === 0){
        return 0
    }
    let res = 0
    const n = height.length
    for(let i=0; i<n-1; i++){
        let lmax = 0, rmax =0
        for(let j=i; j<n; j++){
            rmax = Math.max(height[j], rmax) //右边柱子
        }
        for(let j=i; j>=0; j--){
            lmax = Math.max(lmax, height[j])
        }
        res += Math.min(rmax, lmax) - height[i]
    }

    return res
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 2、暴力枚举优化

时间复杂度：O(n)
空间复杂度：O(n)

//for循环抽出
function trap1(height=[]){
    if(height.length === 0){
        return 0
    }
    let res = 0
    const n = height.length
    let lmax = new Array(n)
    let rmax = new Array(n)
    lmax[0] = height[0]
    rmax[n-1] = height[n-1]
    
    for(let i=1; i<n; i++){
        lmax[i] = Math.max(lmax[i-1], height[i])
    }
    for(let i=n-2; i>=0; i--){
        rmax[i] = Math.max(rmax[i+1], height[i] )
    }
    for(let i=0; i<n; i++){
        res += Math.min(lmax[i], rmax[i]) - height[i]
    }

    return res
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 3、双指针

时间复杂度：O(n)
空间复杂度：O(1)

function trap2(height=[]){
    if(height.length === 0){
        return 0
    }
    let res = 0
    const n = height.length
    let lmax= height[0]  //左边指针移动截止处，左边的最大值
    let rmax= height[n-1] //右边指针移动截止处，右边的最大值
    let left =0, rigth = n-1
    while(left<right){
        lmax = Math.max(lmax, height[left])
        rmax = Math.max(rmax, height[rigth])
        if(lmax < rmax){ //指针移动，只添加较小部分值
            res += lmax - height[left]
            left++
        }else{
            res += rmax - height[rigth]
            right++
        }
    }
    return res
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22